LES ÉNONCÉS 25/01/2008
Exercice 1. On tourne (6e et 5e)
Pour remplir un quadrillage de 366 sur 366 cases, on écrit successivement les lettres R, A, L, L, Y, E dans cet ordre. On commence dans la case située en haut à gauche et on tourne en spirale dans le sens des aiguilles d'une montre (voir le modèle ci-contre avec un quadrillage de 5 sur 5).
Antoine s'arrête lorsqu'il a fait un seul tour.
Bertrand s'arrête lorsqu'il a écrit la 2008e lettre.
|
R
|
A
|
L
|
L
|
Y
|
|
L
|
Y
|
E
|
R
|
E
|
|
L
|
|
|
A
|
R
|
|
A
|
|
|
|
A
|
|
R
|
E
|
Y
|
L
|
L
|
Quelle est la dernière lettre écrite par Antoine ?
Quelle est la dernière lettre écrite par Bertrand et où est-elle placée ?
Exercice 2. Dagobert et son T-shirt à l'envers (6e et 5e)
Dagobert a gagné un T-shirt sur lequel est inscrit « RALLYE 2008 ». Hélas, ce T-shirt est beaucoup trop grand pour lui! Pour amuser ses copains, il l'enfile comme un short en mettant ses jambes dans les manches. En se regardant dans un miroir, il s'aperçoit que le T-shirt est à l'envers (dedans/dehors) ! L'inscription se lit par transparence, car le coton est mince !
Dessiner ce qu'il voit dans le miroir.
Exercice 3. Des diagonales bien embrochées (6e et 5e)
Pour l'apéritif, Ben a fabriqué un gros cube avec 125 petits « Apéricubes ». Il plante alors des grandes piques à brochette selon toutes les diagonales du gros cube.
Combien restera-t-il d'Apéricubes non transpercés ?
Exercice 4. Les gourmands ! (6e et 5e)
Le petit Julien a réuni tous ses amis de classe pour son goûter d'anniversaire. S'étant comptés, les invités ont décidé de lui offrir chacun autant de chocolats qu'il y aura d'enfants autour de la table. Julien a reçu 650 chocolats.
Combien a-t-il d'amis dans sa classe ?
Exercice 5. Le jour "D" (Tous)
Le professeur NESDJOWOİ qui ne sait jamais quel jour on est, s'est fabriqué un jeu de 2 dés, lui permettant d'afficher tous les jours du mois de 01 à 31, écrits en caractères digitaux : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
La date du jour se lit sur les faces de devant. Mais comme les deux dés se reflètent dans un miroir posé sur le bureau, voici ci-contre, ce qu'il voit aujourd'hui.
Trouver tous les chiffres qui sont inscrits sur chacun des deux dés, en expliquant votre raisonnement.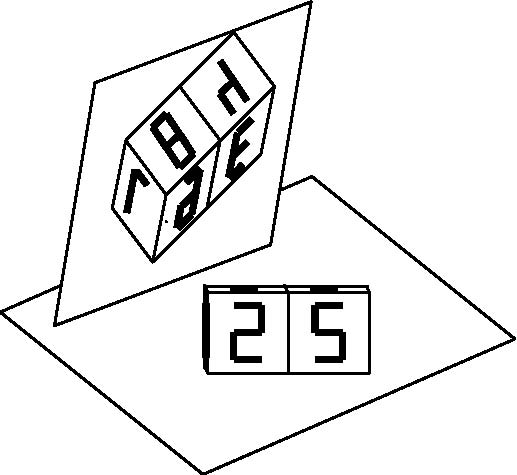
Exercice 6. Le laboureur et ses enfants (Tous)
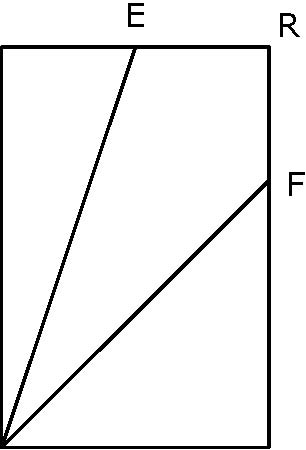
Un riche laboureur, partage son champ de forme rectangulaire, entre ses trois enfants, chacun devant avoir accès au puits situé en P.
En plaçant E au milieu de [AR] et F au tiers de [RC] à partir de R,
- - son fils Alfred, aurait la parcelle PAE d'aire 1 680 m²,
- - son second fils René aurait la parcelle PERF,
- sa fille Cléopâtre aurait la parcelle PCF dont le côté
[PC] mesure 70 m. Ce partage est-il équitable ? Sinon que conseillez-vous de modifier pour qu'il le devienne ?
Évidemment le notaire souhaite que toutes les réponses soient justifiées.
Exercice 7. Le jardinier et la couturière (Tous)
À chacun des sommets d'une pelouse de forme triangulaire, nos deux jardiniers amateurs, Marie et Louis ont planté un arbre : un abricotier (A), un cerisier (C) et un pommier (P). Pour regarder les fruits mûrir, ils décident de mettre un siège (S) sur le bord de la pelouse, entre le cerisier et l'abricotier.
Louis se souvient des cours de mathématiques et se dit que ce serait rigolo de placer ce siège de telle façon que les triangles CPS et APS aient le même périmètre.
Depuis longtemps, il sait bien qu'entre C et A il y a 12 m, entre A et P il y a 16 m et entre P et C il y a 20 m, mais aujourd'hui il n'a sur lui aucun instrument de mesure !
Toutefois Marie qui est bonne couturière, trouve dans sa poche une bobine de gros fil. Louis observe longuement cette bobine, et dit à Marie : « Cela fera l'affaire car il y a certainement plus de 50 m de fil. Tu vas m'aider à utiliser ce fil pour reporter les longueurs comme avec un compas, ainsi je suis certain de trouver la bonne position du siège. »
Comment va-t-il s'y prendre pour déterminer la position exacte du siège ?
Mais quel est donc le périmètre commun aux deux triangles ?
Exercice 8. Un gros cube, des petits cubes... (Tous)
Pour son anniversaire, Camille MAXİCUBE a reçu cette année, par convoi exceptionnel, un cadeau très encombrant contenant 2 008 petits cubes en bois de 1 cm d'arête, empilés les uns sur les autres ! Elle se demande bien comment faire entrer cela dans sa chambre. Elle essaie d'en ranger un maximum en formant le plus gros cube possible.
Quelle est la taille de ce gros cube ? Va-t-il entrer dans sa chambre ? Avec les éléments restants, elle essaie à nouveau de réaliser le plus gros cube possible. Et ainsi de suite.
Finalement comment ses 2 008 cubes sont-ils rangés ?
Exercice 9. PARİS - SÈTE par TROYES. (4e et 3e)
La compagnie de transport CARHİBOU (qui roule même la nuit) utilise trois cars identiques qui sont chacun remplis aux trois quarts. Les passagers occupent donc les trois quarts de trois cars ! Deux tiers des passagers des trois cars descendent à TROYES. Un seul car suffit alors pour transporter les passagers restants. Maintenant au repos, les deux tiers des chauffeurs des trois cars peuvent donc boire un demi avec un tiers inconnu qui se demande quelle fraction du car de SÈTE occupent les passagers. Donnez-lui la réponse en la justifiant.
Exercice 10. Le Trapézien. (4e et 3e)
Pour fêter les dix ans d'existence de son magasin, un pâtissier invite ses principaux clients et fournisseurs.
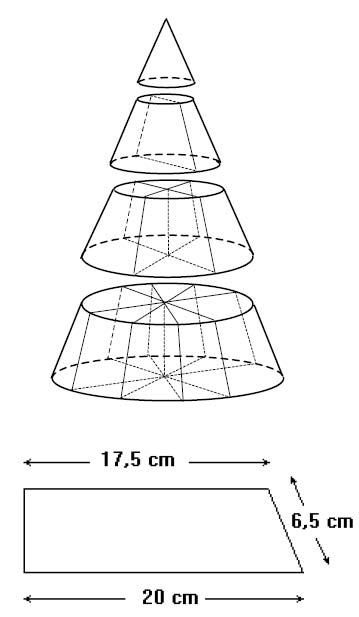
Il confectionne un cône glacé géant au chocolat qu'il
découpe horizontalement en tranches de hauteurs égales.
L'étage supérieur constitue une part. Ensuite, il coupe verticalement le reste des étages : il fait deux parts égales dans le deuxième, quatre parts égales dans le troisième, huit parts égales dans le quatrième, etc.
À partir du troisième étage, toutes les parts ont deux faces verticales en forme de trapèze rectangle, qui
à l'étage du bas ont les dimensions comme indiqué ci-contre :
En combien de parts le pâtissier a-t-il découpé son cône géant ?
Exercice 11. Lapin sauteur. (4e et 3e)
Jeannot Lapin ne se déplace que par sauts réguliers, tous d'une même longueur supérieure à 5 m. Son terrain de jeu préféré est une petite pelouse circulaire de 10 m de diamètre.
Partant d'un point du bord, il atteint le point diamétralement opposé, en ayant fait exactement 4 sauts. Après chaque saut, il se retrouve exactement sur le bord de la pelouse. İl ne retombe jamais deux fois au même endroit.
Faites le dessin du trajet de Jeannot. Quelle est la longueur de chacun des sauts ?
Exercice 12. Courage, plions. (4e et 3e)
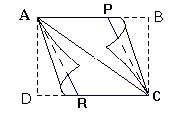
Émilie découpe dans une feuille de papier un rectangle ABCD de 10 cm sur 15 cm. Ensuite elle le plie de façon à amener les largeurs [BC] et [AD] sur la diagonale [AC] (voir figure).
En remarquant que le quadrilatère APCR est un parallélogramme, elle se dit que celui-ci pourrait être un losange, si son rectangle initial avait d'autres mesures.
En gardant la largeur AD = 10 cm, à vous de trouver la longueur convenable du rectangle initial. Quelle est donc la mesure des côtés du losange ?